proving pythagoras theorem using algebraic

Algebraic proofs

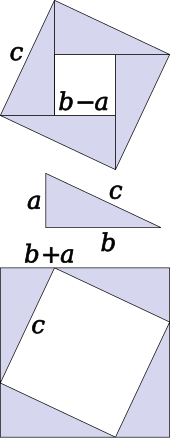
Diagram of the two algebraic proofs

The theorem can be proved algebraically using four copies of a right triangle with sides a, b and c, arranged inside a square with side c as in the top half of the diagram.^[16] The triangles are similar with area , while the small square has side b − a and area (b − a)². The area of the large square is therefore

But this is a square with side c and area c², so

A similar proof uses four copies of the same triangle arranged symmetrically around a square with side c, as shown in the lower part of the diagram.^[17] This results in a larger square, with side a + b and area (a + b)². The four triangles and the square side c must have the same area as the larger square,

giving